Pentagonal polytope
In geometry, a pentagonal polytope[1] is a regular polytope in n dimensions constructed from the Hn Coxeter group. The family was named by George Olshevsky, because the two-dimensional pentagonal polytope is a pentagon. It can be named by its Schläfli symbol as {5, 3n − 1} (dodecahedral) or {3n − 1, 5} (icosahedral).
Contents |
Related star polytopes and honeycombs
The pentagonal polytopes can be stellated to form new star regular polytopes. In two dimensions, this forms the pentagram {5/2}; in three dimensions, this forms the four Kepler–Poinsot polyhedra, {3,5/2}, {5/2,3}, {5,5/2}, and {5/2,5}; and in four dimensions, this forms the ten Schläfli–Hess polychora: {3,5,5/2}, {5/2,5,3}, {5,5/2,5}, {5,3,5/2}, {5/2,3,5}, {5/2,5,5/2}, {5,5/2,3}, {3,5/2,5}, {3,3,5/2}, and {5/2,3,3}. In four-dimensional hyperbolic space there are four regular star-honeycombs: {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5}, and {5,5/2,5,3}.
Family members
The family starts as 1-polytopes and ends with n = 5 as infinite tessellations of 4-dimensional hyperbolic space.
There are two types of pentagonal polytopes; they may be termed the dodecahedral and icosahedral types, by their three-dimensional members. The two types are duals of each other.
Dodecahedral
The complete family of dodecahedral pentagonal polytopes are:
- Edge, {}
- Pentagon, {5}
- Dodecahedron, {5, 3} (12 pentagonal faces)
- 120-cell, {5, 3, 3} (120 dodecahedral cells)
- 120-cell honeycomb, {5, 3, 3, 3} (tessellates hyperbolic 4-space (∞ 120-cell facets)
The facets of each dodecahedral pentagonal polytope are the dodecahedral pentagonal polytopes of one less dimension. Their vertex figures are the simplices of one less dimension.
Elements
| n | Coxeter group | Petrie polygon projection |
Name Coxeter-Dynkin diagram Schläfli symbol |
Facets | Elements | ||||
|---|---|---|---|---|---|---|---|---|---|
| Vertices | Edges | Faces | Cells | 4-faces | |||||
| 1 | 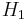 |
Line segment {} |
2 vertices | 2 | |||||
| 2 | 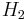 |
Pentagon {5} |
5 edges | 5 | 5 | ||||
| 3 | 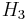 |
Dodecahedron {5, 3} |
12 pentagons |
20 | 30 | 12 | |||
| 4 | 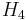 |
120-cell {5, 3, 3} |
120 dodecahedra |
600 | 1200 | 720 | 120 | ||
| 5 | 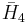 |
120-cell honeycomb {5, 3, 3, 3} |
∞ 120-cells |
∞ | ∞ | ∞ | ∞ | ∞ | |
Icosahedral
The complete family of icosahedral pentagonal polytopes are:
- Edge, {}
- Pentagon, {5}
- Icosahedron, {3, 5} (20 triangular faces)
- 600-cell, {3, 3, 5} (120 tetrahedron cells)
- Order-5 5-cell honeycomb, {3, 3, 3, 5} (tessellates hyperbolic 4-space (∞ 5-cell facets)
The facets of each icosahedral pentagonal polytope are the simplices of one less dimension. Their vertex figures are icosahedral pentagonal polytopes of one less dimension.
Elements
| n | Coxeter group | Petrie polygon projection |
Name Coxeter-Dynkin diagram Schläfli symbol |
Facets | Elements | ||||
|---|---|---|---|---|---|---|---|---|---|
| Vertices | Edges | Faces | Cells | 4-faces | |||||
| 1 |  |
Line segments {} |
2 vertices | 2 | |||||
| 2 | 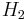 |
Pentagon {5} |
5 Edges | 5 | 5 | ||||
| 3 | 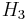 |
Icosahedron {3, 5} |
20 equilateral triangles |
12 | 30 | 20 | |||
| 4 | 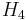 |
600-cell {3, 3, 5} |
600 tetrahedra |
120 | 720 | 1200 | 600 | ||
| 5 | 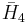 |
Order-5 5-cell honeycomb {3, 3, 3, 5} |
∞ 5-cells |
∞ | ∞ | ∞ | ∞ | ∞ | |
Nots
- ^ Olshevsky, George, [1] at Glossary for Hyperspace.
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25–36]
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Table I(ii): 16 regular polytopes {p, q,r} in four dimensions, pp. 292–293)
| Family | An | BCn | Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regular polygon | Triangle | Square | Hexagon | Pentagon | ||||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| n-polytopes | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes | ||||||||||||